Сумма и произведение

Сумма чисел натурального ряда, произведение ряда чисел

У Васи есть натуральное число n. Он решил представить это число в виде суммы различных натуральных чисел c1 + c2 +... + ck = n, причем количество слагаемых может быть произвольным. При этом Вася хочет, чтобы произведение всех слагаемых, которые встречаются в представлении числа n, было максимально возможным. Помогите Васе и найдите такой набор различных натуральных чисел c1, c2,..., ck, что сумма всех ci равна n, а произведение всех ci максимально возможное. Количество слагаемых в разбиении может быть произвольным.

Входные данные

* В первой строке следует целое число n (1 <= n <= 200) — Васино число.

Выходные данные

* В первую строку выведите два целых числа m и k — максимальное произведение c1 ·c2 ·с3... ck и количество чисел в оптимальном представлении числа n.

* Во вторую строку выведите через пробел k различных натуральных чисел c1, c2,..., ck таких, что сумма всех ci равна n, а произведение всех ci максимально возможное среди всех представлений числа n. Все числа ci можно выводить в произвольном порядке. Если ответов несколько, разрешается вывести любой из них.

Обратите внимание, что для заданных ограничений максимальное произведение помещается в стандартный 64-битный тип данных.

АЛГОРИТМ

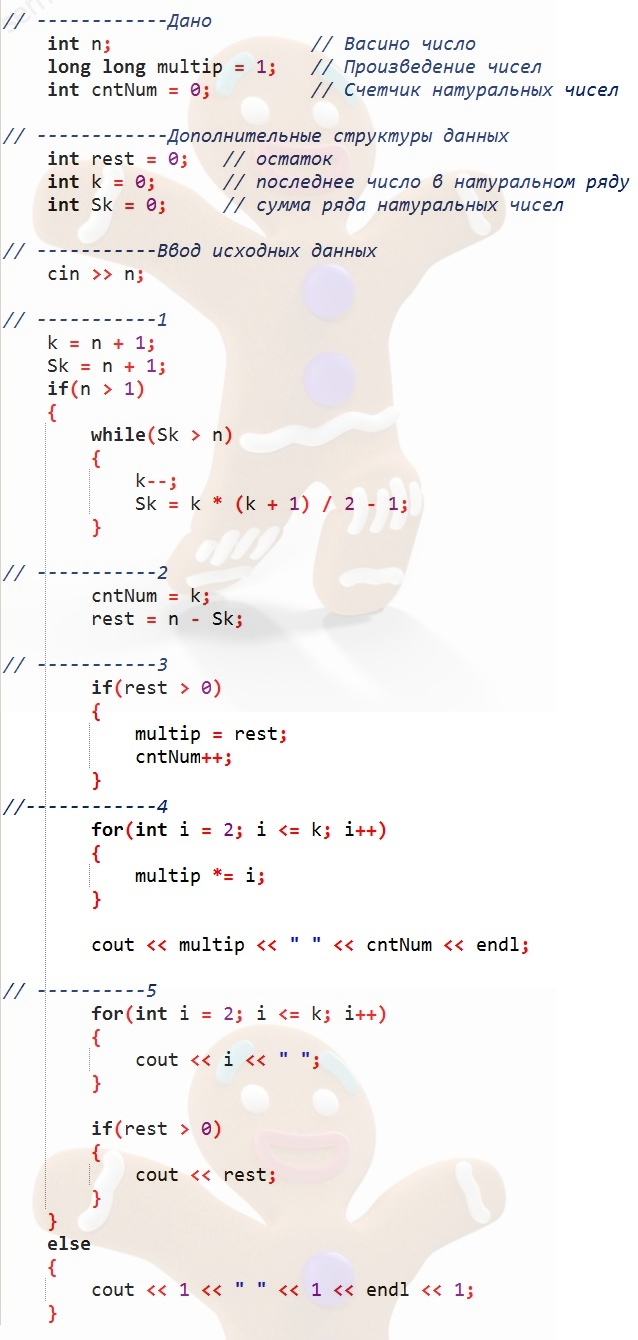
Чем больше натуральных чисел, тем больше их произведение. Число можно представить в виде двух частей n = Sk + rest, где Sk = 2 + 3 + ... + k - сумма ряда натуральных чисел (ряд начали с 2, т.к. 1 не увеличивает произведение) rest - остаток, сколько не хватило до n: rest = n - Sk
1. Если n > 1 (для 1 ответ будем выводить отдельно), используя формулу суммы арифметической прогресии для натурального ряда, определим k - последнее число в натуральном ряде. Начиная с n, будем последовательно уменьшать k и вычислять сумму прогрессии S(k) = k(k + 1) / 2 - 1 пока она не станет меньше или равна n.
   !!! Обратите внимание на -1, т.к. в сумме его у нас нет, а формула для прогрессии учитывает в сумме эту единицу.
2. Cчетчику натуральных чисел присвоим значение k и найдем остаток rest = n - S(k).
3. Если остаток отличен от нуля добавим его к произведению и увеличим cntNum - количество натуральных чисел.
4. Выведем на экран произведение и количество натуральных чисел
5. Выведем натуральные числа от 2 до k. Если rest отлично от нуля, выведем и его