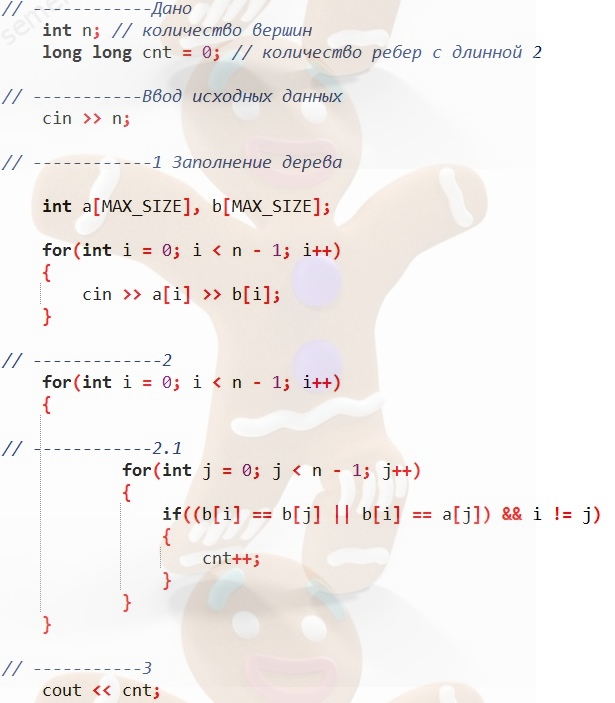
Количество пар
Деревья, поиск элементов массива по значению
Дано неориентированное невзвешенное дерево, состоящее из n вершин. Дерево из n вершин — это граф из n вершин и n - 1 ребра, такой, что между любой парой вершин существует ровно один простой путь (путь называется простым, если он не проходит ни по одному ребру более одного раза).
Определите количество пар вершин (a, b) таких, что a < b и расстояние между вершинами a и b равно двум. Под расстоянием между вершинами понимается количество ребер на пути от одной вершины до другой.
Входные данные
В первой строке следует целое число n (3 <= n <= 2 ·10^5) — количество вершин в дереве.
В каждой из следующих (n - 1) строк следуют по два целых числа ai, bi (1 <= ai, bi <= n, ai != bi) — описание ребер дерева. Гарантируется, что заданный граф является деревом.
Выходные данные
Выведите количество пар вершин (a, b) таких, что a < b и расстояние между вершинами a и b равно двум.
Следует обратить внимание, что ответ в этой задаче может не поместиться в стандартный 32-битный тип данных. Необходимо использовать 64-битный тип данных (long long в С++, int64 в Паскале, long в Java).
АЛГОРИТМ
-
Основная проблема, какую структуру данных выбрать для хранения дерева?
- Заполнение дерева. Дерево строить не будем. Для решения задачи, нам необходимо только знать связи между ребрами.Будем хранить вершины ребер в двух массивах a[i] и b[i], где i - номер ребра.
- Рассмотрим алгоритм на примере:
| i | a | b |
Имеем четыре ребра. Расстояние между вершинами равно двум, если к ребру примыкает еще одно ребро (расстояние между дальними вершинами ребер равно двум).
| 0 | 3 | 1 |
| 1 | 4 | 1 |
| 2 | 1 | 2 |
| 3 | 1 | 5 |
Рассмотрим ребро (3, 1). К нему через вершину {1} примыкает три ребра (4, 1), (1, 2), (1, 5)
Рассмотрим ребро (4, 1). К нему через вершину {1} примыкает три ребра (3, 1), (1, 2), (1, 5)
Рассмотрим ребро (1, 2). К нему через вершину {2} не примыкает ни одного ребра
Рассмотрим ребро (1, 5). К нему через вершину {5} не примыкает ни одного ребраТаким образом получается следующий алгоритм:
2.1 Для каждого ребра, найти сколько раз вершина b данного ребра, встречается в других ребрах и прибавить данное значение к общей сумме